Vittorio Capecchi: Jorge Luis Borges e la matematica

 

 

Con questo testo Vittorio Capecchi ricorda Jorge Luis Borges a trenta anni dalla sua morte avvenuta il 14 giugno del 1986 e festeggia i cinquanta anni della rivista di modelli matematici in inglese che continua a dirigere dal 1966 (Quality and Quantity. International Journal of Methodology edita da Springer Olanda).

 

Quando si  analizza la relazione tra Borges e la matematica è quasi inevitabile partire da un confronto tra Jorge Luis Borges  e Leibniz perché Leibniz  è stato definito “un filosofo borgesiano” e Borges è  giustamente identificato come “un discepolo di Leibniz”.

1. Borges e Leibniz

Nel corso tenuto nel 1980 a Vincennes da Gilles Deleuze su Leibniz[1] Borges viene ricordato per una differenza: in Borges sono compresenti mondi incompossibili  mentre questo non è accettato da Leibniz:

Borges, in Finzioni scrive il racconto “Il giardino dei sentieri che si biforcano”. E’ il libro infinito, il mondo delle compossibilità. L’idea del filosofo cinese alle prese con il labirinto è una idea dei contemporanei di Leibniz. Appare in pieno XVII secolo. Esiste un celebre testo di Malebranches che è l’intervista con il filosofo cinese che contiene cose molto curiose. Leibniz è affascinato dall’Oriente e cita spesso Confucio. Borges ha fatto una copia conforme di Leibniz  ma con una differenza essenziale: per Leibniz, tutti i mondi diversi in cui, che Adamo pecchi in un certo modo o che pecchi in altro modo oppure che non pecchi per niente, una infinità di mondi che però si escludono gli uni con gli altri, sono incompossibili gli uni con gli altri. Tanto è vero che  che mantiene un principio di disgiunzione molto classico: o è in questo mondo o nell’altro. Borges invece, mette tutte queste serie incompossibili nello stesso mondo. Ciò permette una moltiplicazione degli effetti.[2]

Leibniz è invece del tutto d’accordo con Borges perché attribuisce un compito fondamentale ai narratori  e ciò proprio quello di esplorare tutti i mondi possibili proponendo soluzioni e scrive che “nessuno assomiglia  più a nostro Signore che l’inventore di un buon romanzo”. Come scrive Fréderic de Buzon:

[Per Leibniz] il romanzo è dunque storia del possibile, un mondo che ha una sua coerenza nel gioco dei suoi crimini e delle sue sanzioni. L’autrice più vicina alle concezioni di Leibniz è Madeleine de Scudery. Egli trova in Clelia  un esempio significativo di “romanzo dettato dalla ragione” e una armonia di sorprendente intelligibilità. Si noterà una identità dei criteri di armonia quando sono applicati alla produzione dell’arte e alla economia divina: la creazione, se non la Creazione, definisce l’opera romanzesca. Leibniz così scrive a Anton Ulric von Braunschweig: “Tuttavia, uno dei migliori artifici di un autore di romanzi è di lasciare andare tutto verso la confusione e poi trovare soluzioni in maniera inattesa. Nessuno assomiglia di più a nostro Signore dell’inventore di un buon romanzo.[3]

D’altra parte Borges non può che essere d’accordo con Leibniz quando Leibniz scrive nel 1715 il frammento dell’Apokatástasis[4] in cui prefigura il suo racconto La biblioteca di Babele :

Può essere stabilito il Numero di tutti i Libri possibili che non eccedano una grandezza determinata, composti di vocaboli significanti o non significanti; numero che , dunque comprenderà anche tutti i Libri dotati di senso. Chiamo libro di grandezza determinata quello che non superi un numero definito di lettere. Sia per esempio un libro in folio composto 10.000 pagine, e la pagina da 100 linee e la linea da 100 lettere. Il libro risulterà costituito di 100.000.000 di lettere e saranno detti di determinata grandezza i libri che non eccederanno questo numero. Ora il numero dei libri possibili che non superano tale grandezza o se si vuole, di quelli che possono essere formati fino a un  massimo di cento milioni di lettere d’alfabeto è finito. Non solo è finito, ma mediante il calcolo delle combinazioni può essere stabilito il numero possibile dei libri differenti tra loro anche solo di pochissimo, non eccedenti il numero di lettere proposto siano lunghi o brevi.[5]

Daremo, alla fine del quinto paragrafo, la soluzione matematica del  numero totale di libri nella biblioteca immaginata da Leibniz. In questa sede possiamo fare un altro esempio di testi di Leibniz che potrebbero essere scritti da Borges. Jonathan Wichmann[6] indica questi due passi  della Monadologia:

68. E benché la terra e l’aria inframmezzate alle piante del giardino o l’acqua inframmezzata ai pesci dello stagno, non siano né pianta ne pesce, tuttavia ne contengono a loro volta, ma perlopiù d’una sottigliezza per noi impercettibile. 69. Così non vi è nulla d’incolto, di sterile, di morto nell’universo, non vi è caos ne confusione se non in apparenza, pressapoco come potrebbe esservene in uno stagno a una distanza tale da scorgere un movimento confuso e, per così dire, un brulichio di pesci nello stagno, senza distinguere i pesci stessi.[7]

Leibniz sottolinea che si è immersi in uno spazio non percepibile che sta tra il molto piccolo (le monadi unità di vita non visibili) e l’infinito dell’universo e Borges, che si muove in tutti i suoi scritti tra mondo visibile e invisibile, concorda con questo modo di vedere la realtà.

In sintesi si può affermare che le convergenze tra Leibniz e Borges sono nella  “fantasia senza freni inibitori” come sottolinea  Armando Massarenti[8] nella sua introduzione al volume su Leibniz da lui curato che ha come titolo “I sogni borgesiani di Leibniz”:

Anche su un altro scrittore, Jorge Luis Borges, hanno avuto un duraturo effetto gli innumerevoli scambi epistolari, gli articoli brevi su problemi enormi (perché esiste qualcosa invece del nulla ?), gli schizzi intellettuali buttati giù per puro divertimento dal filosofo.  Al punto che, leggendo Leibniz, a volte sembra proprio di leggere Borges. Leibniz è un autore modernissimo, che scrive nel pieno della rivoluzione scientifica e del trionfo del meccanicismo. Ma come ha messo bene in luce Massimo Mugnai, uno dei più importanti studiosi al mondo del suo pensiero, la sua fantasia filosofica non ha freni inibitori, e il suo equilibrio, la sua chiarezza filosofica non ha freni inibitori, e il suo equilibrio, la sua chiarezza e il suo rigore su nutrono anche delle visioni che la Nuova Scienza sembrava contraddire.[9]

I libri di Massimo Mugnai [10]a cui Massarenti fa riferimento comprendono la sua introduzione all’opera di Leibniz  in tre volumi (curata insieme a Enrico Pasini) da cui emerge questa sua anima “borgesiana”. Il filosofo e storico della scienza Paolo Rossi, morto all’inizio del 2012 e autore di un importante libro su Leibniz[11], ha recensito  l’opera di Mugnai concludendo:

Essa è utile anche a tutti coloro che amano sia i testi che parlano dei grandi (così detti “eterni”) problemi, sia quelli che prospettano problemi un po’ strani. Del tipo: si può pensare di individuare un alfabeto dei pensieri umani? Si può fare l’inventario di tutte le conoscenze? Si può stabilire il numero di tutti i i libri possibili? Siamo certi che non si ripeterà minuziosamente la vita dei singoli e che io, seduto in una città chiamata Firenze, posta lungo il fiume Arno, non tornerò a scrivere questa stessa recensione? (per Leibniz la città era Hannover, il fiume Leine, la recensione una lettera)[12]

Come  spesso capita quando viene iniziata una ricerca (in questo caso la relazione tra Leibniz e Borges) c’è sempre qualche studioso che decide di affrontarla in modo sistematico. Stiamo parlando di Herbert H. Knecht, dell’Ecole Polytechnique Fédérale di Losanna che aveva già pubblicato nel 1981 una pregevole monografia su Leibniz[13] in  cui lo definiva dotato di un “surplus di senso non penetrabile da una intellettualità schematica”:

Il pensiero di Leibniz rappresenta una struttura architettonica alla quale la lingua barocca che parla, conferisce colore, musicalità, calore, caratteristiche della vita. (..). Il Barocco si presenta nell’opera di Leibniz attraverso un insieme di tratti, di immagini, di forme, di soggetti (..) uno spettacolo visionario che gli conferisce  un surplus di senso che sarebbe non penetrabile da una intellettualità schematica. L’approccio dell’opera di Leibniz esige  di  lasciarsi  sedurre dal suo charme emotivo che testimonia una simpatia per la cultura barocca nell’abbagliante diversità delle sue realizzazioni[14]

Venti anni dopo Knecht riprende questa valutazione dell’opera di Leibniz come “spettacolo visionario” in un lungo saggio[15] che distingue tra un fantastico senza controlli (che si anima di oggetti magici, fate potenti, gnomi malefici ecc..) e un fantastico razionale (che fa entrare chi legge in una realtà diversa e ha un suo rigore formale). La tesi di Knecht è che si sia in presenza di questo secondo tipo di fantastico e che “l’opera di Jorge Luis Borges illustri perfettamente ai nostri occhi questo prolungamento del progetto inconsapevole di Leibniz verso i suoi limiti fantastici”[16] Una volta presa questa direzione si trovano molte conferme. Knecht inizia con il considerare le somiglianze tra i due autori nelle esperienze di lavoro e nello stile di vita e di studio:

Leibniz ha avuto una lunga carriera di bibliotecario a Hanovre e a Wolfenbuttel, e Borges a Buenos Aires (..) A un livello più personale l’uno e l’altro sono dei solitari, unici nel loro tempo, del tutto personali, uomini privati con la stessa concezione con cui altri si considerano uomini pubblici, nonostante il desiderio continuo di comunicare, una apertura senza riserve sul mondo, una curiosità appassionata e universale . Nelle loro due opere ciò che colpisce immediatamente è il ricorso al mondo del  sapere: allusioni, citazioni, discussioni critiche.[17]

Vengono poi considerati i temi comuni e il comune atteggiamento verso la ricerca:

Numerosi temi infine sono comuni ai due pensatori: quello del labirinto che è senza dubbio fondamentale in tutta l’opera borgesiana sia  sul piano formale dello stile narrativo che al livello di motivo letterario (..) C’è una forte analogia nei temi affrontati, una identità di preoccupazioni che li avvicina, lo stesso meravigliarsi di fronte al concatenarsi aggrovigliato  delle cause e degli effetti dove ogni accadimento ha una sua giustificazione, la stessa fascinazione davanti alle ramificazioni senza limiti del possibile, le stesse meditazioni su gli innumerevoli paradossi dell’infinito, la stessa genialità combinatoria spesso al servizio di una tematizzazione dell’assurdo, una propensione ludica alla mistificazione, l’adesione ai metodi della scoperta scientifica.[18]

In sintesi, scrive Knecht , “per una felice circostanza, Leibniz ha trovato in Borges un prolungamento fantastico che niente faceva presagire. Niente se non questo altro paradosso che risulta da una inversione dei termini che ci fanno vedere in Leibniz il poeta e in Borges il filosofo”[19] Knecht, dopo un dettagliata disamina delle diverse tematiche dei due autori conclude considerando il tema  dell’infinito. Il suo è un invito a rileggere il Leibniz borgesiano:

[in Leibniz che tratta il tema dell’infinito] si compie un’avventura insolita dell’immaginazione nel luogo dell’assurdo, del fantastico, dell’impossibile, nello spazio inquieto del non cosciente, nel dominio inconfessabile e indicibile del respinto. Ma è allora che avviene la sfida imperiosa lanciata alla ragione superba che si prende la sua rivincita nel  riflettere su i suoi limiti. D’altra parte non è stato Leibniz a definire le matematiche come la scienza dell’immaginazione? (..) Al di à di ogni ragionamento possibile, l’irrazionale è permanente e inevitabile (..) E allora rileggete Leibniz.. e sognate! [20]

 

2. Borges e la perpetua corsa di Achille contro la tartaruga

Borges parla degli “immediati e accessibili incanti delle matematiche”[21] e afferma: “molte delle mie idee le ho prese da libri di logica e  di matematica che non ho compreso perfettamente; non sono mai stato in grado di capire completamente questi libri”[22]. Carlo Toffalori ha così spiegato perché Borges amava la matematica: “non nella sua capacità di spargere certezze ma di seminare dubbi”:

In ogni caso, a spulciare tra le pagine di Borges, balza subito evidente una cosa : che la matematica  che vi affiora e che piace allo scrittore argentino è la più più lontana possibile dagli stereotipi e dai preconcetti di una scienza sistematica , coerente e complessa  come la sognava Hilbert.(..)Il fascino che la Matematica esercita su Borges non consiste nelle sue certezze definite ma piuttosto nei suoi enigmi e nei suoi paradossi; non nella capacità di elargire sicurezze ma in quella di spargere dubbi.[23]

Per spiegare questo rapporto tra Borges e la matematica viene analizzato il suo celebre racconto La perpetua corsa di Achille contro la tartaruga partendo dal commento dato da Piergiorgio Odifreddi che ha dedicato a Borges tre saggi[24] . Odifreddi  inizia  la sua analisi di La perpetua corsa di Achille contro la tartaruga riportando le parole con cui Borges descrive il paradosso di Zenone di Elea, la cui “limpidezza non esclude l’impenetrabilità”, e lo spiega affermando che gli Eleatici  riuscirono a definire il paradosso perché ad Achille e la tartaruga sostituirono “due tartarughe messesi d’accordo nel fare la stessa specie di passi o di atti simultanei, per non raggiungersi mai” :

Le implicazioni della parola gioiello – preziosa piccolezza, delicatezza non soggetta alla fragilità, facilità somma di trasporto, limpidezza che non esclude l’impenetrabilità, fiore per gli anni – la rendono di uso legittimo qui . Non conosco migliore qualifica per il paradosso di Achille tanto indifferente alle decisive confutazioni che da più di ventitre secoli l’aboliscono, che ormai possiamo salutarlo immortale. Le ripetute visite al mistero che tale lunga durata postula, le sottili ignoranze a cui essa ha invitato l’umanità, sono generosità di fronte alle quali non possiamo non sentire gratitudine. Viviamolo ancora una volta, anche se solo per convincersi di perplessità e di intimo arcano.[25]

Achille, simbolo di rapidità, deve raggiungere la tartaruga, simbolo di lentezza. Achille corre dieci volte più veloce della tartaruga e le concede dieci metri di vantaggio. Achille corre quei dieci metri e la tartaruga corre un metro; Achille percorre quel metro, la tartaruga percorre un decimetro; Achille percorre quel decimetro, la tartaruga percorre un millimetro; Achille il millimetro, la tartaruga un decimo di millimetro e così all’infinito; di modo che Achille può correre per sempre senza raggiungerla. Fin qui il paradosso immortale.[26]

L’illusione degli Eleatici nasceva dalla identificazione  di questa serie di atti individuali sui generis, con lo spazio omogeneo che li sorregge. Siccome questo spazio può essere diviso e ricomposto secondo una legge qualunque, si credettero utilizzati a rifare il movimento totale di di Achille, ma con i passi di tartaruga. Ad Achille che inseguiva una tartaruga sostituirono in realtà, due tartarughe regolate l’una su l’altra, due tartarughe messesi d’accordo nel fare la stessa specie di passi o di atti simultanei, per non raggiungersi mai.[27]

Ma Borges, come sottolinea Odifreddi, va oltre l’esposizione/spiegazione del paradosso di Zenone e  lo utilizza in due direzioni: il paradosso come un “attentato non solo alla realtà dello spazio bensì a quella del tempo” e il paradosso come svelamento di un dato tipo di “idealismo”:

Il paradosso di Zenone di Elea, come osservò James, è un attentato non solo alla realtà dello spazio ma a quella più invulnerabile e sottile del tempo (.. ) Zenone è incontestabile, a meno di confessare l’idealità dello spazio e del tempo. Accettiamo l’idealismo, accettiamo l’accrescimento concreto di quanto è percepito, e potremo eludere il brulicare di abissi del paradosso[28]

Odifreddi scrive che “Così Borges ammette ciò che tutti gli idealisti ammettono, il carattere allucinatorio del mondo, ma fa ciò che nessun idealista ha fatto: trova nella dialettica di Zenone l’irrealtà in grado di confermare tale carattere. I paradossi non sono dunque per lui problemi da risolvere, come furono ancora per Russell, bensì indizi da usare come saranno da Gödel in poi”.[29] C’è così una terza direzione con cui, per Odifreddi, Borges considera il paradosso. Il mondo ha un carattere allucinatorio ma il paradosso non solo fa emergere la presenza dell’idealità del tempo e dello spazio ma inserisce nella sua architettura “tenui ed eterni interstizi di assurdità” che ne svelano la finzione:

Noi (la indivisa divinità che opera in noi) abbiamo sognato il mondo. Lo abbiamo sognato resistente, misterioso, visibile, ubiquo nello spazio e fermo nel tempo; ma abbiamo ammesso nelle sua architettura tenui ed eterni interstizi di assurdità, per sapere che è finto.[30]

A questo punto Odifreddi si volge ad oriente in cui l’uso del paradosso, come nel buddhismo zen, viene utilizzato per ricercare il proprio vuoto interiore. In che modo si possono far incontrare lo spazio/tempo di Achille con quello della tartaruga: non è logico.  Ma, sempre seguendo Odifreddi, la relazione visibile /invisibile è più complessa. Nascosto dal paradosso c’è infatti un luogo protetto in cui, come nel racconto di Lewis Carroll che Borges ricorda, dopo la  stancante corsa Achille può dialogare con affetto con la tartaruga e questa storia  è così bella che il dialogo viene proseguito da Hoffstadter nel suo libro Gödel, Escher, Bach: un’ Eterna Ghirlanda Brillante [31] oppure ci si può appassionare alla sua trascrizione pittorica: Convesso e concavo nella litografia di Escher del 1955:

 

 

3. Borges e i labirinti

I testi di Borges sono quelli “classici”  Il giardino dei sentieri che si biforcano ed Esame dell’opera di Herbert Quain[32] e, in questo caso, la forma di cui si discute è il labirinto. Apparentemente potrebbe sembrare una variazione della litografia di Escher sopra ricordata ma non è così. La relazione concavo/convesso, come quella tra Achille e la tartaruga è tra due tempi/spazi diversi.  Ne Il giardino dei sentieri che si biforcano il racconto presenta anche una relazione a due: tra il cinese dottor Yu Tsun (ex professore di inglese alla Hochschule di Tsingtao e bisnipote di Ts’ui Pen) e il sinologo inglese Stephen Albert (che è stato anche missionario a Tientsin). La relazione, come tutti sanno, finisce con l’uccisione di Albert da parte di Yu Tsun secondo le regole di una spy story ma il racconto di Borges va oltre questa storia a due e approfondisce il significato di labirinto.

Quando si considera un labirinto fisico quali interrogativi si pongono? Prendiamo ad esempio il labirinto di Robert Morris costruito nel 1982 nella fattoria di Celle a Santomato di Pistoia  riprodotto in una serigrafia dello stesso autore:

 

 

 

 

 

 

 

Come scrive Alessandra Acocella un labirinto può  essere visto da due punti di vista: quello dell’artefice e quello di chi inizia a percorrerlo:

Del termine labirinto, nella sua accezione spaziale, può essere data una duplice definizione, a seconda del punto di vista adottato nel rapportarsi ad esso.
Nell’ottica dell’artefice il labirinto è una struttura architettonica della quale egli “ha equilibrato l’effetto di inganno e l’effetto di seduzione negli aggrovigliamenti, nelle ramificazioni, nelle giravolte e nei ritorni”[1].
Al contrario per chi vi s’imbatte, ignaro del disegno complessivo dell’intricato percorso, il labirinto è lo spazio che si mostra progressivamente per parti davanti ai suoi occhi, una volta varcata la soglia ed iniziato l’ignoto cammino.
Il punto di vista del creatore, totalizzante e onnicomprensivo, è paragonabile a quello di un osservatore che contempla da un luogo distante e sopraelevato. La visione dall’alto riduce l’articolata figura geometrica ad un insieme afferrabile nella sua complessità, ne svela l’intima logica e composizione[2]

Nel racconto di Borges il labirinto a cui si fa riferimento è un  labirinto di simboli, ma ci sono ugualmente i due punti di vista prima ricordati: quello del lettore /visitatore che racconta le sue esperienze soggettive  percorrendo il labirinto e quello dell’osservatore che, “da un punto di vista distante e sopraelevato” cerca di ricostruire la forma del labirinto voluta dal suo autore.

Il primo punto di vista è stato scelto da Ethan Weed[3] che ha  letto il  testo di Borges come se dovesse “muoversi attraverso un labirinto per esplorare uno spazio sconosciuto” e il risultato di questa sua esperienza  è che si tratta di un labirinto senza centro come nella litografia di Escher Up and Down:

 

I labirinti dei testi medievali erano complessi, ma avevano un centro che poteva trovare un assiduo lettore ben preparato a quel viaggio. Invece nel Giardino dei sentieri che si biforcano non è possibile trovare un  singolo, incontestabile centro, ma piuttosto molti possibili centri nessuno dei quali è completamente soddisfacente per un lettore che cerchi di scoprire il messaggio nascosto. La storia non permette al lettore di cambiare prospettiva per vedere il labirinto dall’esterno. Chi legge, innocente, per la prima  volta il testo è lasciato con l’impressione che c’è qualcosa che non capisce, qualcosa che deve aver dimenticato. Questa impressione rimane anche in chi legge la storia più volte. (..) Se c’è un centro nel Giardino dei sentieri che si biforcano consiste esattamente nello stesso tipo di di indecisione che trovo quando sono al centro della litografia di Escher Up and Down. E’ un tipico labirinto con un’unica via in cui il soggetto entra, passa molto vicino al centro ma non può saperlo perché il sentiero lo porta lontano prima di ritornare al centro (..) Un labirinto è un posto che non si può lasciare e se lo si lascia è per la stessa porta per cui si è entrati.[4]

 

Se si osserva Up and Down di Escher del 1947 si tratta di una immagine diversa da quella Convesso e concavo prima ricordata. In tutte e due   è rappresentato un labirinto senza un centro ma mentre nella prima c’è una relazione tra due tempi/spazi diversi nella seconda c’è la circolarità di uno stesso tempo/spazio che differisce per alcuni dettagli. C’è un’immagine al tempo t di un uomo sulle scale che parla a una donna alla finestra e la stessa immagine al tempo t+1 senza poter stabilire quale immagine viene prima e quale dopo: due immagini di un “invisibile labirinto di tempo”[5].

Gabriel Screiber e Roberto Umansky[6], a differenza di Weed, cercano di porsi da un punto di osservazione esterno e, come Odifreddi, cercano un appoggio nella matematica per interpretare questi due testi di Borges. La loro analisi porta a sottolineare che i tempi plurimi e ramificati di cui parla Borges sono rintracciabili nei testi scientifici di Poicaré e Prigogine:

 

La teoria matematica della biforcazione trae origine  dall’opera di Henri Poincaré su i sistemi di equazioni differenziali non lineari. Il termine biforcazione fu coniato da Poincaré  per indicare l’emergere di più soluzioni da una data soluzione. Ogni volta che la soluzione di una equazione o sistema di equazioni cambia qualitativamente a seconda del valore di un parametro, detto valore critico, si ha il fenomeno della biforcazione. Il punto dello spazio dei parametri dove avviene tale evento è detto punto di biforcazione (..) L’idea della biforcazione è centrale nelle teorie della fisica contemporanea delle termodinamica irreversibile. Il contributo della scuola di Prigogine a questo proposito sono di importanza primaria mostrando che le biforcazioni, sotto condizioni di equilibrio far-from, costituiscono il naturale meccanismo di evoluzione e di raggiungimento di complessità[39].

C’è quindi una identità di vedute tra i due testi di Borges e quelli di Poincaré e Prigogine fino alle recenti teorie di un Caos in cui all’interno è possibile individuare un ordine. Screiber e Umansky analizzano anche le relazioni  tra Borges e la teoria dei frattali di Mandelbrot e concludono scrivendo che “Borges preferisce trattare di biforcazioni e aspetti del caos che hanno a che fare con il tempo piuttosto che trattare di geometrie frattali che hanno a che fare con lo spazio” [40]

 

4. Borges e la ricerca di infinito

L’ interpretazione prima ricordata converge con quella di Italo Calvino che precisa le tre ipotesi del tempo proposte da Borges: un idea di tempo puntuale, un idea di tempo dominata dalla volontà, un’idea di tempo plurimo e ramificato:

Le ipotesi sul tempo che vengono proposte nel Giardino dei sentieri che si biforcano, ognuna contenuta (e quasi nascosta) in poche righe, sono: un’idea di tempo puntuale, quasi un assoluto presente soggettivo (“..riflettei che ogni cosa, a ognuno, accade precisamente, precisamente ora. Secoli e secoli, e solo nel presente accadono i fatti: innumerevoli uomini nell’aria, sulla terra e sul mare, e tutto ciò che realmente accade, accade a me..”); poi un’idea di tempo determinato dalla volontà, il tempo di una azione decisa una volta per tutte, il cui futuro si presenti irrevocabile come il passato; e infine l’idea centrale del racconto: un tempo plurimo e ramificato in cui ogni presente si biforca in due futuri, in modo da formare “una rete crescente e vertiginosa di tempi divergenti, convergenti e paralleli”. Questa idea di infiniti universi contemporanei in cui tutte le possibilità vengono realizzate in tutte le combinazioni possibili.[41]

Calvino  termina il saggio citando un passo di Borges che vede in questi  infiniti mondi possibili il confine che separa il mondo, che vive nel tempo reale, dal mondo che vive nel tempo più ambiguo della letteratura e dell’arte:

Nel tempo reale, nella storia, ogni volta che un uomo si trova di fronte a varie alternative opta per una ed elimina o perde le alte; non così nell’ambiguo tempo dell’arte, che somiglia a quello della speranza e dell’oblio.[42]

La biblioteca di Babele e La teoria dei cicli di Borges[43] permettono ulteriori precisazioni. Floyd Merrell[44] ha presentato una interpretazione matematica de La biblioteca di Babele in cui rileva la sintonia di Borges con le posizioni metodologiche  di Feyerabend o della così detta interpretazione di Copenhagen della teoria dei quanti e conclude affermando che Borges ne La Biblioteca presenta “uno scenario di incertezze generalizzato” anche perché ogni modello, e non solo quello della Biblioteca, è fiction.

Borges, come Feyerabend e i teorici della RMV (Radical Meaning Variance) in generale, mettono in guardia su i limiti del mondo e sulla povertà della nostra concezione del mondo. La Biblioteca e le altre costruzioni di Borges demoliscono l’universo di Newton che fa emergere le diverse antinomie. Ma Borges non vuole un’altra “realtà”  che lo sostituisca. Piuttosto egli contrappone una nuova perdita di certezza nei confronti delle vecchie certezze verso uno scenario di incertezza generalizzato. Katherine Hayles[45] sottolinea che in generale la fiction di Borges “differisce dai modelli scientifici utilizzando il concetto che ogni cosa, inclusa la realtà, è fiction” mentre per contro “i modelli scientifici sono utili perché in qualche misura riflettono la realtà”. Anche se  considero il saggio della  Hayles brillante  penso che sia complessivamente errato: Nietzche, Vaihinger e i teorici della RMV e la maggior parte dei “nuovi fisici” vedono correttamente tutti i modelli come fiction. O, per parafrasare Werner Heisenberg[46], tutte le teorie non sono della realtà ma della interazione della nostra mente con la realtà.[47]

C’è però, in questo scenario di incertezza, la ricerca di infinito che sostituisce la precedente immagine di labirinto e in questa direzione è interessante ripercorrere il percorso di Escher nei suoi diversi tentativi di rappresentarlo.

In un articolo pubblicato nel 1959 Escher spiegò che ciò che lo spingeva a rappresentare l’infinito (che esiste “eternamente nel tempo e interminabilmente nello spazio”)  era il superare l’angosciante idea del “senza spazio”, il “nulla” (che è diverso dal vuoto):

L’uomo è incapace  immaginare che in un qualche punto al di la delle stelle più lontane nel cielo notturno lo spazio possa avere fine, un limite oltre il quale non v’è che il nulla. Il concetto di “vuoto ha per noi un certo significato, perché non possiamo almeno visualizzare uno spazio vuoto, ma il nulla, nel senso di “senza spazio” è al di la della nostra capacità di immaginazione. E’ per questo che da quando l’uomo è venuto a giacere, sedere, stare in piedi, a strisciare e camminare senza terra, a navigare, cavalcare e volare sopra di essa (e lontano da essa), ci siamo aggrappai a illusioni, a un al di là, a un purgatorio, un cielo e un inferno, a una rinascita o un nirvana, che esistono tutti eternamente nel tempo e interminabilmente nello spazio.[48]

All’inizio, come precisa Bruno Ernst[49],  Escher utilizzò la forma quadrata e vennero fatte le xilografie da Sviluppo II del 1939 a Sempre più piccolo I del 1956 (la prima xilografia riprodotta nella sequenza sotto riportata) in cui la ricerca di infinito è risolta nel rappresentare i grandi rettili ai bordi della xilografia sempre più in piccolo via via che vanno verso il centro (“la bisezione delle figure è stata portata all’assurdo. L’animale più piccolo avente ancora una testa, una coda e quattro zampe, è lungo circa 2 mm“). Per lo spettatore l’infinito è visto, come nel racconto Una discesa nel Maelström di Edgar Allan Poe, dai bordi di un gorgo in cui si è trascinati oppure, come Escher suggerisce, come un’infinità sequenza di figure che nascono in un punto lontano, imprecisato, e prendono a poco forma per poi diventare visibili e grandi accanto allo spettatore.

 

 

 

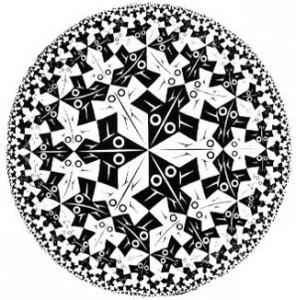
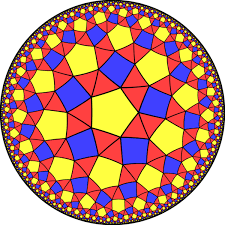
Ma Escher a proposito della xilografia Sempre più piccolo scrive che “dal punto di vista della composizione questo lavoro è solo in parte soddisfacente” e cerca altre soluzioni che gli verrano dall’incontro con il matematico Harold Scott Macdonald Coxeter che gli gli fece conoscere il Disco di Poincaré che è un modello di geometria iperbolica  realizzato dal matematico francese Jules Henri Poincaré: quando questo disco viene tassellato tramite triangoli iperbolici si ha la configurazione  a colori  (la seconda nella sequenza sopra riportata) ed il bordo del disco va  verso l’infinito. Coxeter inviò ad Escher  una sua comunicazione del 1957 inviata alla Royal Society del Canada[50] che conteneva una figura ed Escher ne rimase molto colpito. Escher  iniziò a realizzare le xilografie Limiti del cerchio I, II, III, IV di cui riproduciamo la III (la  terza nella sequenza sopra riportata) e così Escher commenta la xilografia Limite del cerchio III realizzata nel 1959:

Nella xilografia a colori Limite del cerchio III sono state eliminate del tutto le imperfezioni di Limite del cerchio I. Si hanno ancora  soltanto gruppi di “traffico scorrevole”, tutti i pesci che appartengono a un insieme e hanno uno stesso colore e nuotano uno dietro l’altro, lungo un binario circolare. (..) Salgono verticali da lontananze infinite come razzi, partendo dalla circonferenza e di nuovo ci ripiombano, non una sola componente raggiunge mai il confine . Poiché al di là vi è il nulla assoluto. Eppure questo mondo circolare non può sussistere senza il vuoto che lo circonda – non solo per il fatto che un dentro presuppone un fuori , ma anche perché gli immateriali archi della circonferenza sono ordinati in modo strettamente geometrico nel nulla.

La stessa xilografia è commentata da Coxeter[51] nel 1979 che descrive in questo testo anche come sono iniziati i suoi rapporti con  Escher :

Ho incontrato Escher nel settembre del 1954 quando una esposizione dei suoi lavori fu sponsorizzata dal Congresso Internazionale di Matematici ad Amsterdam di quell’anno. Nei precedenti 17 anni aveva realizzato disegni (..) con due innovazioni rimarcabili: l’unità base (in genere un singolo animale o la metà di un animale simmetrico o due differenti animali) è ripetuta  non solo per traslazioni ma anche per altre isometrie (o trasformazioni congruenti): rotazioni, riflessi, riflessi con scorrimento; queste ripetizioni sono realizzate ingegnosamente senza che vi siano interstizi. Nel linguaggio della matematica (disciplina di cui Escher si proclama risolutamente “ignaro di conoscenze”) questa unità di base è una regione fondamentale per un gruppo simmetrico). In una lettera del dicembre 1958 mi scrisse: “La ringrazio (..) per il suo testo sulla “Crystal Symmetry and its Generalizations” (..) e specialmente la figura 7 di pagina 11 [ la terza figura riprodotta nella sequenza sopra riportata] mi ha procurato uno shock. Da molto tempo sono interessato a modelli con motivi che diventino sempre più piccoli fino a che non raggiungano i limiti di una infinita piccolezza”.

Coxeter in questo testo analizza on dettaglio la simmetria non euclidea presente nella xilografia Limite del cerchio III e se si vuole capire come Escher sia riuscito a realizzare questa xilografia si può leggere il testo di Bill Cassellman[52] disponibile in rete.

 

5. Borges e la biblioteca di Babele

I rapporti di Escher con la matematica sono simili a quelli di Borges ma la ricerca di infinito che entrambi portano avanti è diversa. Per capire questa diversità viene ricordata l’interpretazione de La biblioteca di Babele fatta dal logico matematico Carlo Toffalori sulla base dei due teoremi di incompletezza dimostrati da Kurt Gödel nel 1931:

La biblioteca di Babele (..) Lo spunto iniziale è ben noto: si tratta di una biblioteca “interminabile”, i cui scaffali sembrano raccogliere qualsiasi possibile combinazione-sensata o insensata- di lettere dell’alfabeto, così che a “righe ragionevoli” e “notizie corrette” si alternano sovrabbondanti e impenetrabili “cacofonie, farragini verbali e incoerenze”. Di questo universo “informe e caotico” ogni interpretazione è possibile. I mistici possono cercarvi “il libro ciclico” che “è Dio”, l’uomo comune il senso della propria vita. Si può addirittura pensare che su qualche scaffale compaia “il libro totale”, “la chiave e il compendio perfetto di tutti gli altri”, la rivelazione, la Verità, e a chiunque riesca ad accostarlo sia concesso di diventare “simile a Dio”. Ma la biblioteca può anche prestarsi a un ulteriore interpretazione: perché non supporre che essa non si altro che l’aritmetica, così inaccessibile a ogni umana percezione, e gli affanni di scoprire il “libro totale” corrispondano ai tentativi impacciati di comprendere i fondamenti dei numeri? Così la Biblioteca diventerebbe, e senza forzature alcuna, proprio la figura dei teoremi di incompletezza: un’aritmetica di Babele.[53]

Toffalori segue questa interpretazione della Biblioteca come “aritmetica per comprendere il fondamento dei numeri” e come per questa via si possa  capire che ogni numero ha un suo DNA, un suo “biglietto da visita”.

Tanto per cominciare i numeri naturali possiedono anche loro un  DNA che si presti all’esigenza? Per sorprendente che possa apparirvi, la risposta è si .(..) Ad esempio 120 è 2³ x 3 x 5 e 750 è 2 x 3 x 53 . Ma quando diciamo che 120 è – lui e lui solo-  2³ x 3 x 5 e che non può che decomporsi che così implicitamente affermiamo che quei tre esponenti 3, 1, 1 – nell’ordine in cui si susseguono costituiscono il suo biglietti da visita, la sua carta , l’impronta del suo codice genetico, senza equivoco possibile (..) E’ su questa base che Gödel riusci a numerare ordinatamente lettere, parole, dimostrazioni, ragionamenti. Tra loro tutto diventa numero, come per miracolo, senza confusioni o sovrapposizioni.[54]

Il percorso è ormai tracciato. I numeri, seguendo Gödel, hanno una “sorta di autocoscienza, di autocritica, di capacità di riflettere su se stessi” e, seguendo questo “spericolato” sillogismo, Toffalori può dimostrare che sono “vivi”:

A: sui numeri si possono concepire principi, dimostrare teoremi, formulare dubbi. B: questi principi, teoremi e dubbi sono anch’essi numeri, ma se tutto questo ha senso e fondamento- e fondamento ne ha, come  Gödel ci mostra- non c’è che una conclusione: che i numeri vivono.[55]

La prova visiva  della diversa ricerca di infinito di Escher rispetto a Borges si può  avere immediatamente considerando due disegni della Biblioteca di Babele: quello del francese Philippe Fassier, specialista in disegni di labirinti, e quello della belga Sophie Racine, illustratrice e realizzatrice di film di animazione.

 

 

 

 

 

Per dare una idea di complessiva della Biblioteca di Babele, il disegnatore francese si basa sulla indicazione di Borges di una biblioteca fatta da “un numero indefinito, forse infinito, di gallerie esagonali” mentre la disegnatrice belga si basa su “la scala spirale che s’inabissa e s’innalza nell’ignoto”[56]. Ma la relazione tra ordine e caos non è nella architettura della Biblioteca (come prima era nella architettura del labirinto): é all’interno dei contenuti dei libri. I libri sono vivi in tutte le loro diverse edizioni e copie per cui ogni singolo libro (con quella data edizione, acquistato da quella data persona, collocato in quel dato scaffale ecc..) ha una sua vita, identità e storia. Nella Biblioteca di Babele invece i libri perdono la loro identità e diventano combinazioni di parole per cui in questa Biblioteca ci sono insieme Libri (quando la combinazione di parole ha senso anche se non ha una identità libraria di anno di edizione, copertina ecc..) e Non libri (quando la combinazioni di parole è priva di senso).

La differenza tra la ricerca di infinito di Escher e quella di Borges è che Escher, pur presentando forme tutte uguali come i pesci nella xilografia Limiti del cerchio III, lascia ad ogni pesce una sua possibile identità mentre Borges nella sua Biblioteca mette insieme  Libri e non Libri . L’interpretazione della Biblioteca più corretta è perciò quella di Toffalori che  vede in quella Biblioteca non la vertigine di un numero “indefinito e forse infinito di gallerie” che contengono libri ognuno pronto per essere letto  ma la vertigine di numeri.

Il numero di libri della biblioteca di Babele è stato calcolato da Odifreddi[57] in 25 elevato a 656.000 che equivale a 10 elevato a 900.000 e scriverlo richiederebbe circa 900.000 cifre. Più grande era la biblioteca immaginata nel 1715 da Leibniz[58] (C alla 1000.000.000 dove C è il numero dei caratteri incluso lo spazio bianco) e ugualmente più grande era quella descritta nel 1904 da Kurd Lasswitz[59] (in cui il numero dei volumi è 10 elevato alla 2.000.000). Tutti i volumi di queste biblioteche[60] sono comunque in un numero molto più piccolo del numero di tutti gli atomi che compongono il mondo come ipotizza Borges ne La dottrina dei cicli [61]: questo numero  calcolato da Odifreddi arriva a 10 elevato a 1.000.000.000.000 e, per scriverlo sarebbe necessario  almeno un miliardo di miliardi di cifre.[62] Per avere un’idea di quella che Borges chiama la  “stravagante felicità”[63] di fronte alla vertigine di numeri si può leggere il libro di Bruno D’Amore[64] in cui è ricordato che il valore di π che è 3,14 con 2 miliardi di cifre dopo la virgola. D’Amore, per far capire la “felicità” di cui parla Borges,  riporta  le prime 100.000 cifre di quei due miliardi e il risultato è, come scrive D’Amore, “impressionante”: queste 100.000 cifre prendono più di cinque pagine del libro[65].

 

6.  Borges, l’Yijing  e il sacro

Che relazione si può trovare tra la Biblioteca di Babele con la sua vertigine di numeri e il l’Yijing Classico dei Mutamenti? Questa vertigine è rintracciabile nel numero sempre più elevato di lettori e lettrici che lo consultano da quattromila anni ma, nel Classico dei mutamenti, è presente un’altra situazione: la sacralità dei numeri. La sua origine mitica è intrecciata con il quadrato magico, Bouvet vede nelle sei linee dell’esagramma i sei giorni necessari per la creazione biblica, i 64 esagrammi sono, come ricorda Odifreddi[66] “praticamente lo stesso numero, cioè 63, degli elementi della tavola periodica che Dimitri Mendeleev letteralmente sognò una notte del 1869, dopo aver giocato un solitario prima di addormentarsi”. Inoltre   Cyrille Javary  ci informa che le parole che compongono l’Yi Jing sono 4.082 una cifra  molto vicina a 4.096 che è il prodotto di 64×64 e viene così dimostrato “questo insieme di meticolosità e leggerezza, di perfezionismo e di humour con cui i cinesi dell’Antichità amavano cesellare i loro grandi testi classici”[67]

Di fronte al sacro gli appassionati di matematica (e anche quelli che non la amano)  si dividono. Piergiorgio Odifreddi sul Classico dei mutamenti esprime la stessa ostilità espressa dal grande stuioso della scienza e tecnologia nell’antica Cina  Joseph Needham. Odifreddi parla dell’ Yi Jing come un “libro della sorte” che osa proporre “una chiave per spiegare gli infiniti avvenimenti possibili” attraverso 64 “miseri esagrammi” con “relativi oscuri commenti”:

[C’è una] nutrita schiera dei cosiddetti “libri della sorte” o “della ventura”: di quei testi, cioè, che a partire dal classico cinese I Ching, o Libro dei Mutamenti (Adelphi), millantano, in maniera seria o faceta, di fornire un aiuto divinatorio per districarsi nel casi della vita. Con un approccio ossimorico alla previsione del futuro, essi spesso pretendono di dominarne la necessità attraverso la casualità: affidandosi, cioè, all’estrazione di bastoncini o al tiro di monete [ne]I Ching (..). Come diceva il premio Nobel per la fisica Niels Bohr, però, fare previsioni è sempre difficile, soprattutto sul futuro. Per tutelarsi, i maestri divinatori preferiscono nascondere le loro dietro formulazioni vaghe e generiche, delegandone al fruitore la corretta interpretazione: il che, naturalmente, risulta sempre facile col senno di poi, cioè “dopo” che i fatti sono ormai avvenuti, ma altrettanto sempre impossibile “prima”. D’altronde, come potrebbero i miseri 64 esagrammi dell’ I Ching e i relativi oscuri commenti fornire, da soli, una chiave per gli infiniti avvenimenti possibili, se non attraverso un’interpretazione sfrenatamente creativa? [68]

Chi scrive ama moltissimo gli scritti di Odifreddi e Needham ma ama anche l’Yijing e Borges che ha scritto ottantenne questa poesia Per una versione de I Ching[69]

 

Per una versione de I Ching

L’avvenire è altrettanto irreparabile

Quanto il rigido ieri. Non esiste cosa

Che non sia una lettera muta

Dell’eterna scrittura indecifrabile

Il cui libro è il tempo. Chi si allontana

Dalla propria casa vi è già tornato. La nostra vita

E’ il sentiero futuro già percorso.

Niente ci dice addio. Niente ci lascia.

Non cedere . L’ergastolo è buio.

La dura trama  è d’incessante ferro.

Ma in qualche cantuccio della tua cella

Può esserci una svista, una fenditura.

La strada è fatale come la freccia,

Ma nelle crepe sta in agguato Dio.

 

In questa poesia il Classico dei mutamenti è visto come relazione tra l’esperienza umana (xing) e il destino (ming). Di fronte a una “eterna scrittura indecifrabile il cui libro è il tempo” c’è un destino “irreparabile” che è “fatale come la freccia” ma “in qualche cantuccio” della cella in cui ognuno è collocato “può esserci una svista, una fenditura”, una possibilità di mutamento. Ed è in questa possibilità di mutamento, in questa svista, in questa  crepa che “sta in agguato Dio”.

 

 

 

 

Category: Libri e librerie, Storia della scienza e filosofia